In a recent post (Why Italy? Why Spain? And why the EFSF’s size does not matter), I concluded with a question that readers keep asking: “If what you are saying is right, why are Europe’s leaders so committed to the current structure of the EFSF?” More generally, the world has been watching Europeans blundering incessantly from one spectacular failure to the next and increasingly wonders whether their actions are a manifestation of irrationality or some sinister plan. In that post’s closing paragraph I suggested that there is a third explanation: Europe’s commitment to the awful EFSF, and other such disastrous policies, reflects a most peculiar form of rational idiocy. Today I shall lay bare this explanation by means of four telling illustrations: The Penny Pincher’s Conundrum, The Underbidder’s Nightmare, The Speculator’s Delight, and, lastly, The Eurozone’s Dilemma.
The Penny Pincher’s Conundrum
Imagine we place ten shiny gold sovereigns on a table (since gold is all the rage these days) and invite Angela and Bill to take turns to collect either one or two coins at a time. We tell them that if, at any visit to the table, one of them collects two coins, the game ends and the remaining coins are lost to both. But as long as each collects a single coin, they can keep coming back till all coins are collected.
[We assume that all that Angela and Bill care about is the number of coins that they receive individually, and that no enforceable agreement for sharing the coins ex post is possible.]
What should Angela do if we give her the chance to step up to the table first? Should she take a single coin, thus giving Bill a chance to play too, or take the two of the ten coins and kill the game there and then (thus causing the loss of eight gold sovereigns to both)?
Clearly, the rational outcome would be to collect one coin at the first visit, let Bill do the same at his first visit and keep doing this so that, between them, they do not let a single gold coin go to waste. Alas, this is not what will happen if they allow themselves to think in the manner that economists define as ‘rational’. Why not?
If Angela is smart, she will work out from the outset that, if the game keeps going until only two coins are left on the table (and each one of them has pocketed four), it will be her turn to play and, at that point, she will not be able to resist taking both. But if she respects Bill’s intelligence, she will know that he will have worked out this conclusion too. So, she will quickly conclude that, just before that stage is reached, when there are three coins on the table, and it is Bill’s turn to play, Bill will predict that if he takes only one coin she will then collect two and, therefore, Bill must defend his interests by collecting two coins himself, while he still has a chance.
[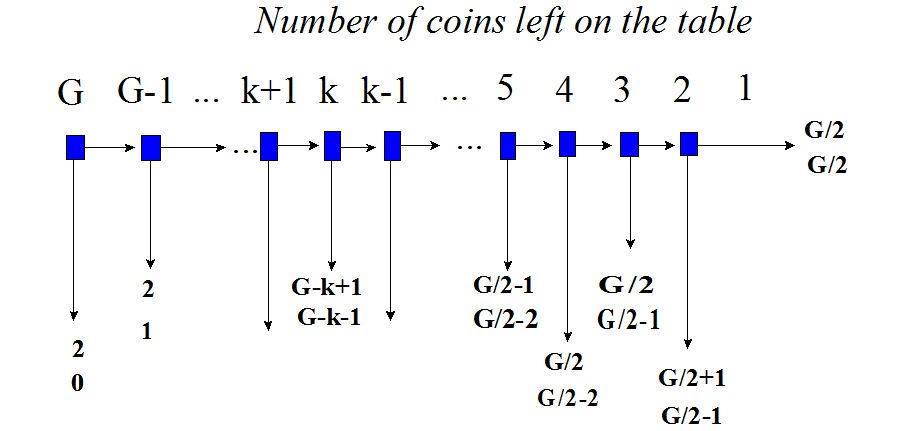 The adjacent figure helps follow her logic’s twists and turns. It generalises to the case where, at the beginning, there are G golden sovereigns on the table. If Angela, who plays first, takes two coins, she follows the vertical arrow downwards. The first number of coins then represents the payoff of the player who took two coins and the second the other player’s tally. Similarly at every stage of the game. Clearly, if they reach the end by taking one coin each, each ends up with G/2 coins.]
The adjacent figure helps follow her logic’s twists and turns. It generalises to the case where, at the beginning, there are G golden sovereigns on the table. If Angela, who plays first, takes two coins, she follows the vertical arrow downwards. The first number of coins then represents the payoff of the player who took two coins and the second the other player’s tally. Similarly at every stage of the game. Clearly, if they reach the end by taking one coin each, each ends up with G/2 coins.]
Smart Angela, therefore, ‘knows’ that if they reach the stage when there are three coins on the table, she will collect none of them (since Bill will pick up two). With this thought in mind, she will ensure that when it is her turn to play with four coins on the table, she must collect two. Then again she knows that Bill will also work this out and thus becomes convinced that he will kill the game (by collecting two coins) before they reach that stage; when he gets to choose with 5 coins on the table. And so on and so forth.
To cut a long story short, Angela has just worked out that Bill will have an incentive (courtesy of his predictions of what she thinks he will do) to pick up two coins whenever he gets a chance; even right after at the game’s beginning. So, Angela predicts that if, at the very beginning, she takes a single coin, he will take two immediately after and the game will end with her having only one gold sovereign. With this firm conclusion in her mind, one that was worked out with superb reasoning and foresight, she steps up to the table and collects two coins on her first visit. Too bad that eight sparkling gold sovereigns have gone to waste…
The story’s moral: Rational choices and infinite strategic foresight offer no defence against collective and individual idiocy. A penny-pincher may end up with pennies in her pursuit of penny maximisation when much greater riches are available. In contrast, a capacity to think in terms of the collective interest would, ironically, serve the decision maker’s private interest much, much better.
The Underbidder’s Nightmare
Angela and Bill now play a new game. We put €100 in a box and allow them to bid for it incrementally (in steps of €1 at a time) but under the following rules: The highest bid wins the box (and its contents) but both the highest and the second highest bids are paid in full. For example, if the bidding ended with Bill offering €60 and Angela €30, Bill wins the €100 but Angela must also pay us €30 as a participant’s fee. It is not hard to see that:
(A) It is always rational to enter the game by making a bid
(B) If both make a bid, the bidding process will continue until both are ruined.
The first conclusion, (A), is quite straightforward: €100 is on offer and, if one’s opponent does not bid, it makes huge sense to bid €1 to get the €100. Beyond that, if the other has made the first move, and bid €1, it makes sense to offer €2.
The second conclusion, (B), seems less self-evident but is equally simple to arrive at logically: The moment one has made any bid, one has a cast iron incentive to bid above the other. Suppose, for instance, that Angela’s €X is surpassed by a €(X+1) bid by Bill. Since she must pay her bid even if she loses the auction, she is better off bidding €(X+2). Why? Because €[100-(X+2)] always exceeds -€(X+2). But note that this is true even if X exceeds €100 by any number! That is, this auction will never end. Both players will be outbidding each other, resembling supremely rational idiots with a penchant for bankruptcy. When will this auction end? Only when one of them hits the buffers of her or his budget constraint. Or when, alas, they start wondering whether their type of rationality needs to be scrutinised…
The story’s moral: It is perfectly possible for policy makers to find themselves in a dynamic situation which compels one constantly to throw good money after bad in pursuit of an impossible objective, with the result that everyone is a loser. When caught in such a dynamic spider’s web, e.g. the EFSF’s dynamic as depicted here, the only rational thing to do is to stop. But then again it takes considerable leadership qualities to subject one’s own rationality to some higher-order scrutiny and lead the Union out of the cul-de-sac.
The Speculator’s Delight
Speculators like nothing more than an official non-credible commitment. Here is the simplest possible depiction of such a feeble assurance.
| Speculator attacks | Officials resist |
3 |
3 |
| Speculator attacks | Officials capitulate |
1 |
2 |
| Speculator desists |
2 |
1 |
|
| Spec’s pref. order | Officials’ pref. order | ||
The idea here is that the speculator will not attack if she has reason to expect that officials will resist (nb. an attack followed by resistance yields the speculator’s third outcome, i.e. corresponds to her least preferred outcome). This may lead foolish officials (e.g. the former Greek Finance Minister, Mr G. Papakonstantinou; recall his threats to speculators that they would “lose their shirts” if they bet against Greek bonds) to threaten speculators with reprisals if they dare challenge them. Why foolish? Because, at least in this case, these threats cannot and will not be taken seriously. And why is that? Because speculators can see that, if they attack, the officials will be forced to choose between an action that yields their second best outcome (capitulation) and another action that yields their third best (i.e. their worst) outcome (resistance). Which action will officials choose? Capitulation of course, just as Europe’s leaders have been doing for the past eighteen months.
Then again, one may argue, quite plausibly, that things change when this ‘game’ between officials and speculators is repeated again and again. That then it may well make sense for officials to resist for a number of periods so as to signal to speculators that they can expect a bloody nose every time they challenge them. In this sense, the short or medium term cost of resisting speculative attacks (i.e. the cost to officials of opting repeatedly for their third, rather than their second, preferred outcome) can be seen as an investment in a reputation that will keep speculators at bay.
This may well be so. Except, to work as a proper deterrent against speculation, it must be commonly known that the officials’ planning horizon is indefinite. That it stretches well into the future. Alas, this is hardly ever true. For we all know that Mrs Merkel’s and Mr Sarkozy’s planning horizon barely stretches to the next local or national election. And since their horizon is known to be definite, even fixed, something like the rational idiocy of the Penny Pincher’s Conundrum applies: Speculators work out that, at some point in the not too distant future (determined by the electoral cycle), the officials will capitulate (just like Angela, in that game, predicts that Bill will collect, sooner or later, two as opposed to one gold sovereigns). Then, by the logic that led Angela to take two coins immediately (see The Penny Pincher’s Conundrum above), speculators predict that the officials’ resolve to take the long view will melt down instantly.
The story’s moral: Speculators can be kept at bay only when officials are not constrained by a finite horizon. Or when the game is changed so that officials’ defensive moves cost them less than capitulation. In Europe, tragically, neither applies. The short term cost of capitulation is lower than the short term cost of resistance while the officials’ horizon coincides with the core countries’ next election.
The Eurozone’s Dilemma
Suppose I am right in my conviction that implementation of The Modest Proposal would end the crisis here and now. Is it possible that, e.g., Mrs Merkel knows this and still chooses, rationally, to resist such a systemic solution? Yes, is my answer.
Suppose, for argument’s sake, that Mrs Merkel agrees with us that a combination of (A) ECB-issued eurobonds that allow for the transfer of the Maastricht compliant debt to the Centre, and (B) bank recapitalisation would resolve the euro crisis. But let us also suppose that she takes it for granted that the bankers will be allowed to make their own decisions on whether they want to draw upon EFSF funds to effect the said recapitalisation (at the expense of equity that will dilute their own holdings). Then it is very possible that we have the following strategic interaction:
| Banks recapitalise | Banks do not recapitalise | |
| ECB-bonds + tranche transfer |
2,3 |
4,1 |
| Current EFSFbased policy |
1,4 |
3,2 |
Europe’s leadership chooses its policy from the two rows whereas the bankers choose from the two columns. The numbers in the table correspond to the ranking of the outcomes of European officials, the first number, and of the bankers, the second number.
The assumption here, which one may of course contest, is that European leaders, with Mrs Merkel first and foremost among them, understand that maintaining the current strategy of EFSF loans for the ‘fallen’ states (let’s call this the EFSF strategy) will lead to their third-best outcome if bankers continue to refuse recapitalisation – notice the bottom right cell in which Europe’s leaders end up with their third best outcome and the bankers with their second best. In contrast, if Europe’s leaders were to go ahead and authorise the ECB to issue its own bonds, while the banks recapitalised, our leaders get their second best and bankers their third best outcome.
As for the worst outcomes possible, for the core countries’ politicians it is that they go ahead with ECB-bonds (and a transfer of the eurozone’s Maastricht compliant debt to the ECB) only to discover that the bankers refused to recapitalise their banks (since that would effect debt unification without stemming the banking crisis that started the whole disaster). And the worst outcome of bankers is that they recapitalise (i.e. lose much of their control over the banks) when Europe is sticking to the toxic EFSF (thus ensuring the crisis’ continuation).
Lastly, the best outcomes are exactly the opposite: For surplus country politicians, it is that the bankers recapitalise without the ECB taking the decisive step toward sovereign debt unification. And for bankers the best outcome is that the ECB unifies the debt, via the issuing of its own eurobonds, without themselves having to recapitalise their banks – notice that in the off-diagonal cells, one ‘player’ gets her least preferred outcome (number 4) while the other gets her most preferred outcome (number 1).
With all these assumptions in place, it is easy to see how instrumental thinking leads both politicians and bankers to a disastrous outcome: Rationally! Let’s start with the banks. If they predict that Europe will adopt the Modest Proposal’s ECB-issued eurobond policy (i.e. the first row), they know that they will get their third best if they recapitalise and their first best if they do not. Also, if they expect that Europe will stick to the toxic EFSF (i.e. that they will be constrained within the second row), bankers know that to recapitalise will yield their fourth-best and not to recapitalise their second best outcome. In short, whether they expect Europe to go ahead with ECB-bonds and the unification of the Maastricht compliant debt, bankers will not recapitalise. Period!
Let us now look at things from the perspective of core, or surplus, country politicians; e.g. Mrs Merkel. She knows, by perusing the table, that if the banks recapitalise, her best option requires that she does not authorise the ECB to issue bonds and unify the Maastricht compliant part of the eurozone’s debt (observe that her number 1 preference lies in the bottom left cell). And if banks are to choose not to recapitalise, ECB-bonds and Maastricht compliant debt unification gives her her worst possible outcome (notice that the top right cell contains her nightmare: preference no. 4). In brief, whatever she expects the bankers to do, to recapitalise or not to recapitalise, Mrs Merkel is best off by sticking to the catastrophic EFSF…
The story’s moral: As suggested in my previous post’s conclusion, it is possible that surplus countries’ politicians are choosing an allegiance to the EFSF and related policies even if they know that this commitment is tantamount to a poor, even a catastrophic, choice. In this illustration we saw how a particularly narrow way of thinking rationally, what philosophers refer to as ‘instrumental rationality’, leads to an outcome that is, at once, (a) terrible for Europe’s politicians and (b) impossible for their logic to escape.
Overall moral
The difference between good and bad leadership boils down to a capacity to transcend the penny pincher’s logic. True leaders know how not to undermine their own interest by learning to resist the temptation presented by the prospect of small net political gains. Inspired politicians know not only how to manoeuvre skilfully within a game’s rules but, primarily, how to re-write the rules. Unfortunately, Europe’s politicians are proving a breed that has risen through the hierarchy of their parties and parliaments by adapting themselves brilliantly to the existing games, utterly incapable of transcending either instrumental thinking or the game itself. While things were going swimmingly, prior to 2008, this narrow-minded, instrumental, rationality sufficed. After the Crash of 2008 it no longer does.
Postscript
For the purposes of this post I had to delve into my game theoretical past. Masochistic readers who want to read more on game theory, its uses and abuses, may benefot from a book I published in 2004 by Routledge (jointly with Shaun Hargreaves Heap) entitled: GAME THEORY: A critical text.














